引言

储罐通常配备二级防护设施，例如安全提，以控制储罐故障后溢出的液体，安全堤系统由围墙形成，具有各种形状。通常，围墙是垂直的，但有时围墙会被建成为梯形横截面的土堤，以便于火防护设备进入罐区，其侧面和水平面会有倾斜角度。对于危险液体，例如液化天然气（LNG）等危险材料的液化天然气（LNG）储罐，安全堤系统是极为重要的，因为溢出的LNG倾向于在低沸点温度下迅速蒸发，安全堤可以减少LNG与空气和地面的接触面积减少热传导从而降低蒸发速率。有些法规要求对堤岸设计采用110％的规则；但是，在发生灾难性的储罐故障后，即便符合此规则的安全堤设计可能也无法容纳所有液体，造成某些液体会从安全堤壁上溢出，从而造成严重的漫堤事故。

一些学者基于灾难性储罐故障研究的实验结果，开发了漫堤分数预测模型。 Greenspan和Johansson（1981）进行了实验室规模的实验来研究漫堤分数，即漫堤液体与罐中原始液体的质量比。在这个系列实验中，他们使用气缸来快速提起储罐来模拟储罐的灾难性故障，储罐中的液体被立即释放。他们发现，漫堤率取决于无量纲变量的组合，如式（1）所示。

Q=Q(h/H,r/H,R/H,θ)

如图1所示，其中h是安全堤的高度，H是罐内液体的高度，r是安全堤的等效半径，R是储罐的半径以及θ是安全堤壁的倾角。

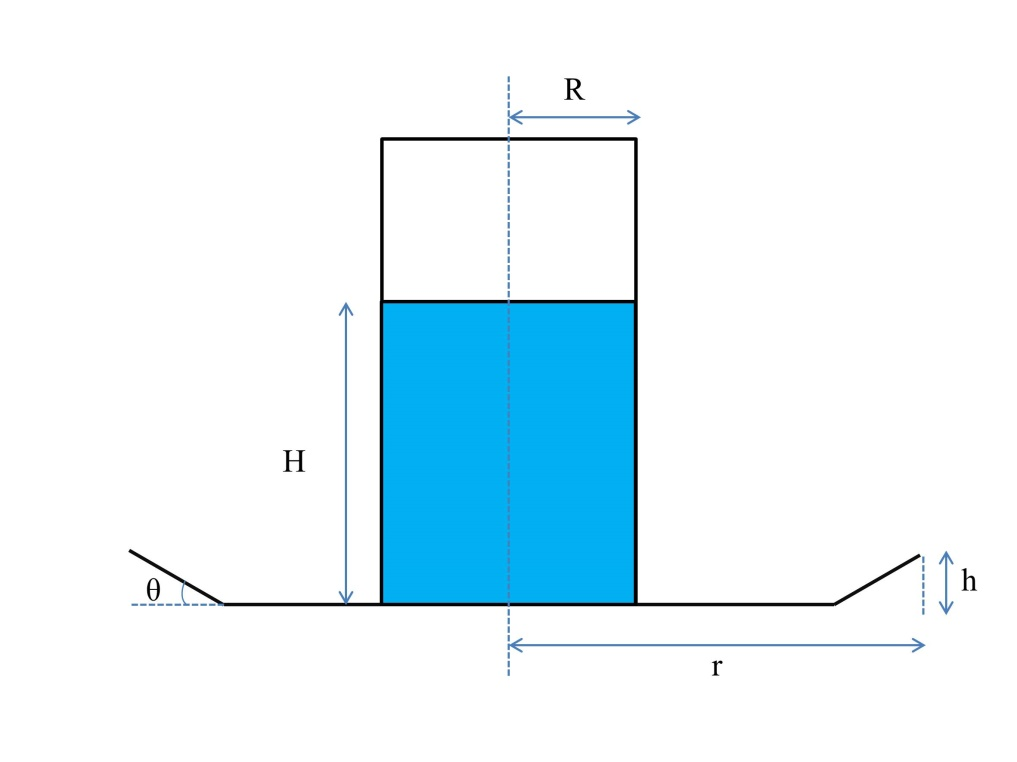
图1：储罐与安全堤参数

Clark et al. (2001) 根据Greenspan 和 Johansson(1981)的实验数据提出了如式(2) 所示的预测模型来预测漫堤分数

Q=exp⁡[-p(h/H)]

当θ= 90°时，p = 3.89; 当θ= 60°时，p = 2.43; 当θ= 30°时，p = 2.28。在0.33 ≤ [(r-R)/R] ≤ 4的条件公式成立

Hirst (Thyer et al., 2002)利用相同的实验数据提出了不同的方程形式，他认为漫堤分数Q主要是由ln（h/H）和ln（r/H）决定的如式（3）所示。

Q=A+Bln⁡(h/H)+Cln⁡(r/H)

当θ= 90°时，A = 0.044，B = -0.264，C = -0.116; 当θ= 60°时，A = 0.287，B = -0.229，C = -0191; 当θ= 30°时，A = 0.155，B = -0.360，C = -0.069。

利物浦约翰摩尔大学（LJMU）受健康与安全执行局（HSE）委托进行了一系列实验，模拟了具有各种形状的障壁的储罐的灾难性故障(Atherton, et al., 2007; Atherton, 2005)。他们提出了另一个公式来预测垂直储罐的超载比例圆形障壁，如式（4）所示。该模型可以更好地预测漫堤分数，但是形式很复杂。

Q=1.0255-2.9551(h/H)-0.816(r/H)+0.3842(R/H)+2.7535(h/H)²+0.0140(r/H)²-0.0637(R/H)²-0.8595(h/H)³-0.0005(r/H)³

先前的工作仅使用了少量实验数据，没有包括倾斜角参数，且未能验证其对其他形状的堤岸的性能。这项工作收集了所有关于漫堤实验研究的报道数据，并用它们为圆形堤，方形堤和任意形状的安全堤开发了新颖的漫堤分数预测模型。这些预测模型使用多种统计绩效指标进行了评估。研究结果被用来为安全堤设计和未来工作提供建议。

方法

为新的漫堤分数预测模型选择变量是至关重要的。Greenspan和Johansson（1981）的工作已经确定了关键变量，包括储罐中的液体高度（H），储罐半径（R），堤岸高度（h）和堤岸等效半径（r）以及安全堤倾角θ，其中液位（H）是影响超标率的最显着变量。 因此，在本项工作中，它被用作分母，以h / H，r / H和R / H的形式使所有其他变量无量纲化作为参数引入方程式中，另外将θ也作为一个因变量加入方程之中，这样便可预测不同角度的漫堤分数。模型参数确定以后，方程形式需要通过大量尝试来获得，通过尝试指数函数、对数函数等不同方程形式的拟合，其中几种相关性较好的方程形式如式（5-7）所示

式中A B C的值是通过MATLAB回归函数拟合实验数据确定的，引入倾斜角参数cosθ，拟合圆形堤实验数据得到圆形堤预测模型即式（5）

Q=-0.3195ln⁡(h/H)-0.3031ln⁡(r/H)+0.2782ln⁡(R/H)+0.1174+0.4200cosθ

同理拟合方形堤实验数据可得到方形堤预测模型即式（6）

Q=-0.2283ln⁡(h/H)-0.2688ln⁡(r/H)+0.1665ln⁡(R/H)+0.1564

最后由于存在不规则安全堤，因此使用所有漫堤实验数据拟合得到无限制预测模型式（7）

Q=-0.2180ln⁡(h/H)-0.1534ln⁡(r/H)+0.0861ln⁡(R/H)+0.1479+0.3018cosθ

结果

将新颖的模型与现有模型进行比较以显示改进的性能。 Greenspan和Johansson（1981），Atherton（2005）和Zhang等人的实验测量。将实验测量值作为水平坐标，将每个模型的预测值作为垂直坐标。在某些情况下，预测模型可能会提供负值，这在物理上是不可能的，因为漫堤分数不能为负。因此，在负的预测值的情况下，漫堤分数设置为零。图中对角线上的点表示完美的预测；对角线下方绘制的数据点表示预测不足；否则，预测值高于测量值。虚线表示±50％的误差。圆形堤预测模型对比如图2所示。

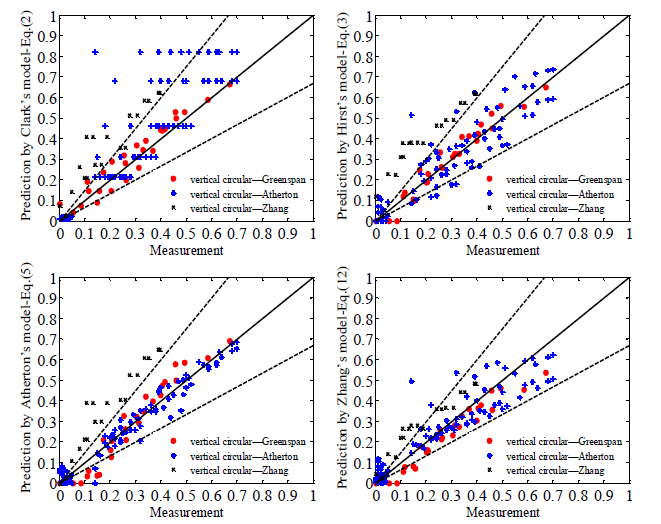
图2 圆形堤预测模型

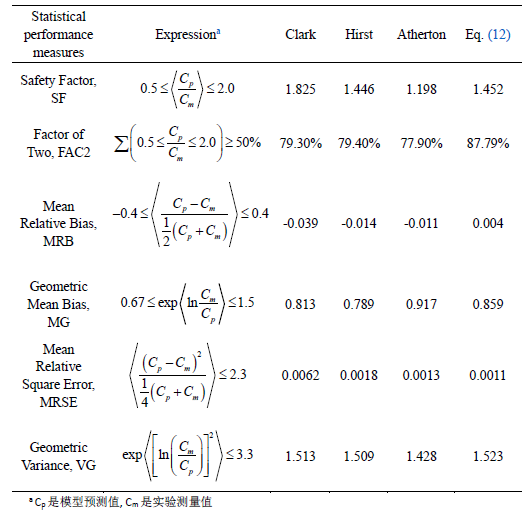
除了利用图来直观对比模型的预测性能外，统计性能度量表能更为准确的对模型预测能力进行评估，六个常用的统计性能参数被选用作为主要参数来评估预测模型，结果如表一所示，与其他模型相比，新模型被认为提供了最佳预测，因为它是表一六项统计绩效指标中的三项中最好的。 其中，FAC2是最可靠的度量，因为它不受高低异常值的过度影响。 SF，MG，VG受极低值的强烈影响，并且未定义为零值，将更适用于预测浓度和观测浓度均变化许多数量级的数据集。 有时，有必要对数据施加最小阈值。 在当前的研究中，有许多数据的超标率低于5％，并且没有使用最小阈值进行分析，因此，该新模型对SF，MG，VG不太好，但仍接近所有模型中的最佳模型。

表一 垂直圆形漫堤模型的统计性能度量

如圆形堤所示，倾斜堤、方形堤和不规则形状堤都采用类似的方法进行一一对比分析，在此不做过多的赘述。

结论

通过回顾灾难性储罐故障堤岸过顶的实验研究，根据所有报告的数据，开发了新的漫堤分数预测模型以预测具有圆形障壁，方形障壁和任意形状的障壁的灾难性储罐故障的漫堤比例。包含倾斜角（θ）有助于开发漫堤分数预测的合并模型，而不是每个倾斜角的特定模型。通常，由于使用了更多的数据来对模型进行回归，因此与基于统计性能指标的先前模型相比，预测精度有所提高。这项工作中第一次开发了方形安全堤模型。不管模型的形状和倾角如何，该通用模型都证明是可行的。另外法规强制执行的“ 110％规则”可能有效地控制了灾难性储罐故障后的堤岸超车，但是需要使用本研究开发的模型对每个特定案例进行分析，以确保堤岸性能。

参考文献